一、什么是平衡二叉树
1.概述
平衡二叉树(AVL树)是一种带有平衡条件的二叉搜索树。它的特性如下:
- AVL树的左右两个子树的高度差的绝对值不超过1
- AVL树的左右两个子树都是一棵平衡二叉树
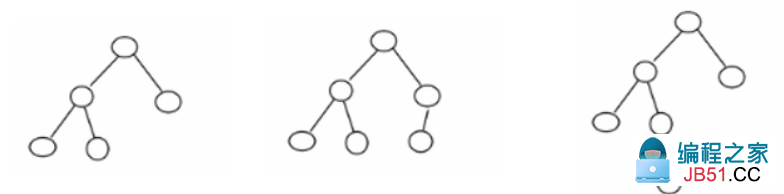
举个例子,如上图所示:
- 第一棵树左树高2,右树高1,差值为1,是一颗AVL树;
- 第二棵树左树高2,右树高2,差值为0,是一颗AVL树;
- 第三棵树左树高3,右树高1,差值为2,不是一颗AVL树;
红黑树就是一直AVL树。
2.为什么需要平衡二叉树
当我们使用二叉排序树的时候,当连续插入顺序的节点的时候就会出现问题。比如,我们插入{1,2,3,4,5}这样一个数组:
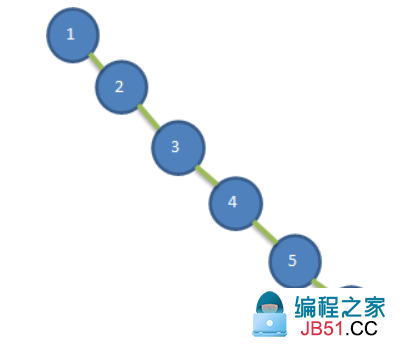
可见该树左树节点全为空,比起树更像单链表,这也导致了该树的插入和查询速度明显的下降,查询速度甚至因为每次多处一个比较左树的操作导致还不如单链表。为了避免这种情况,我们引入的AVL树。
二、AVL树左旋转
1.思路分析
AVL为了避免左右树高度差超过1,在可能导致这种情况的插入或者删除操作时会进行旋转。
我们举个例子,现在有数列{4,6,5,7},当插入8后,现在的得到的排序树如下图:
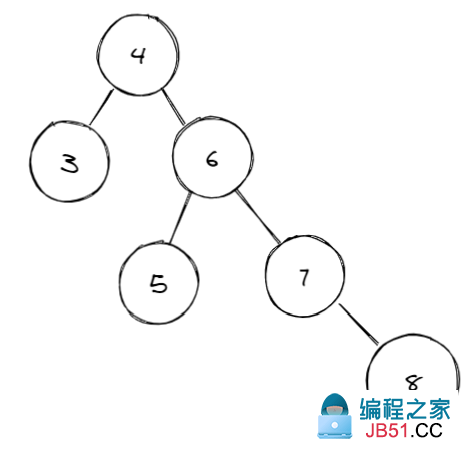
明显不再是一个AVL树,所以需要进行左旋转:
-
我们以当前根节点值再创建一个新节点
newNode -
让新节点的左子节点指向根节点的左子节点
newNode.left = root.left -
让新节点的右子节点指向根节点的右子节点的左子节点
newNode.right = root.right.left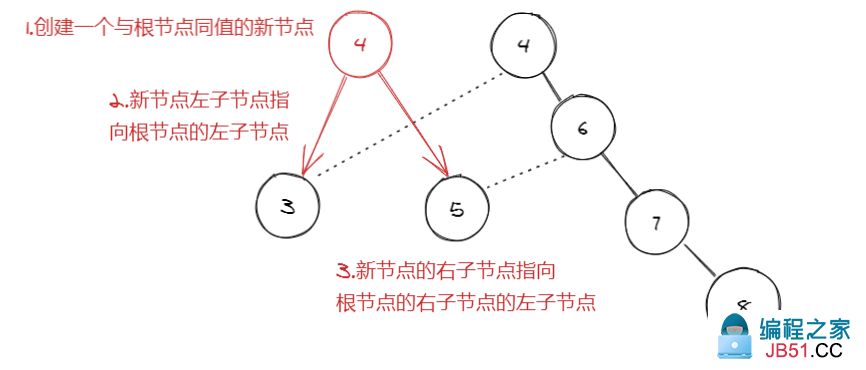
-
把根节点的值换成右子节点的值
root.val = root.right.val -
把根节点的右子节点指向其右子节点的右子节点
root.right = root.right.right -
让根节点的左子节点指向新节点(根节点的右子节点成为了新的根节点)
root.left = newNode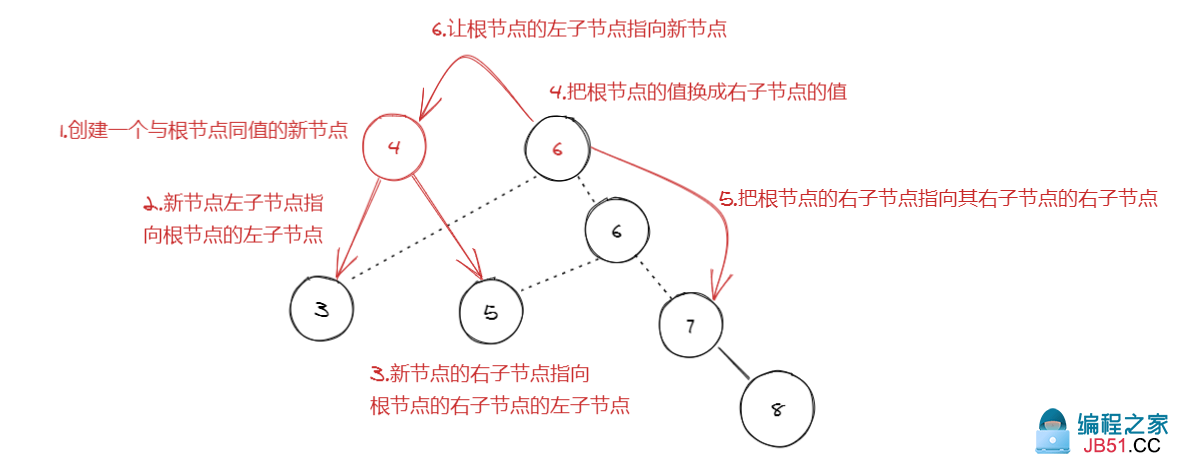
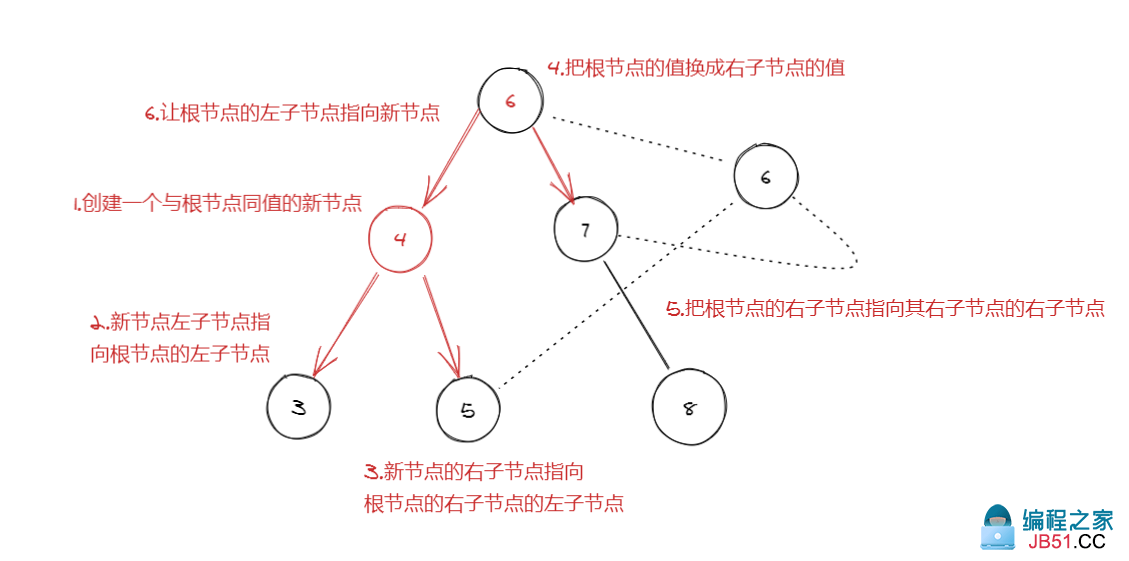
我们调整一下图片样式,就可以直观的看到左旋转后树的样子:
网上看到一个非常形象直观的动图:
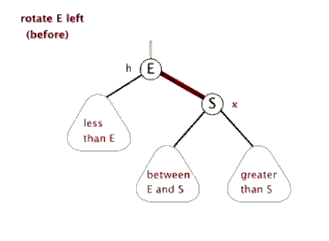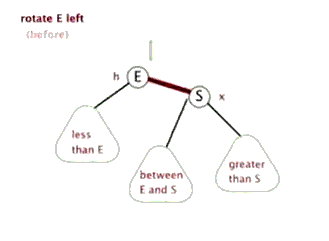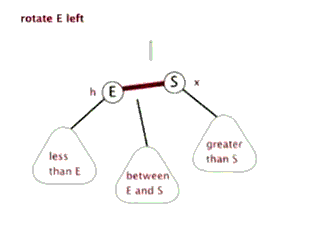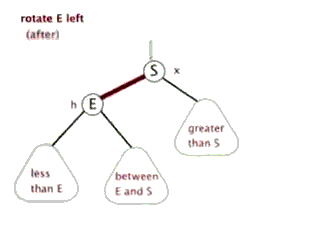
不难理解:左旋的目的是降低左子树的高度
2.代码实现
由于AVL树是基于BST改进的一种数据结构,所以这里的AVL树类继承了BST的方法和代码,使用同一个节点类,这里具体的代码可以参考之前的文章。
我们先创建一个继承BST的AVL树类:
/**
* @Author:CreateSequence
* @Date:2020-07-23 19:01
* @Description:平衡二叉树
* 由于是在二叉排序树的基础上改进,这里直接继承了二叉排序树类
*/
public class AVLTree extends BinarySortTree{
public AVLTree(BinarySortTreeNode root) {
super(root);
}
}
由于旋转的条件是左右子树高度差大于1,所以我们需要有几个方法来判断树的高度:
/**
* 获取当前节点的右子树高度
* @param node
* @return
*/
public int getRightHeight(BinarySortTreeNode node) {
if (node.right == null) {
return 0;
}
return getHeight(node.right);
}
/**
* 获取当前节点的左子树高度
* @param node
* @return
*/
public int getLeftHeight(BinarySortTreeNode node){
if (node.left == null) {
return 0;
}
return getHeight(node.left);
}
/**
* 获取以当前节点为根节点的树高度
* @param node
* @return
*/
public int getHeight(BinarySortTreeNode node) {
//判断当前节点的左/右节点是否为空,是返回0,否则遍历返回当前节点的左右树最高值
return Math.max(node.left == null ? 0 : getHeight(node.left),node.right == null ? 0 : getHeight(node.right)) + 1;
}
/**
* 排序树左旋转
*/
private void leftRotate() {
// 1.创建新节点,与根节点值相同
BinarySortTreeNode node = new BinarySortTreeNode(root.val);
//2.让新节点左子节点指向根节点左子节点
node.left = root.left;
//3.让新节点的右子节点指向根节点的右子节点的左子节点
node.right = root.right.left;
//4.让根节点的值变为其右子节点的值
root.val = root.right.val;
//5.把根节点的右子节点指向其右子节点的右子节点
root.right = root.right.right;
//6.让根节点的左子节点指向新节点
root.left = node;
}
当添加完一个节点后,我们判断左右子树的高度差是否大于1,如果是就进行左旋
/**
* 重写二叉排序树的节点添加方法,当添加完节点后左子树与右子树高度差大于1时,让树进行左旋转,若情况相反则进行右旋转
* @param node
*/
@Override
public void add(BinarySortTreeNode node) {
super.add(node);
//添加完节点后,判断左子树与右子树高度差是否大于1
int disparity = getRightHeight(root) - getLeftHeight(root);
if (disparity > 1) {
System.out.println("高度差:" + disparity + ",左旋转!");
//左子树与右子树高度差大于1就左旋
leftRotate();
}
}
注意:截止目前,仅仅只对左子树高度较高的情况作了处理!
三、AVL树的双旋转
左旋转是为了降低左子树的高度,但是如果是右子树高度过高,我们就需要右旋,事实上,一个完整的AVL树,应当是能够双旋的。
右旋的步骤与左旋基本一致,但是方向不同:
-
我们以当前根节点值再创建一个新节点
newNode -
让新节点的右子节点指向根节点的右子节点
newNode.right = root.right -
让新节点的左子节点指向根节点的左子节点的右子节点
newNode.left = root.left.right -
把根节点的值换成左子节点的值
root.val = root.left.val -
把根节点的左子节点指向其左子节点的左子节点
root.left = root.left.left -
让根节点的右子节点指向新节点(根节点的左子节点成为了新的根节点)
root.right = newNode
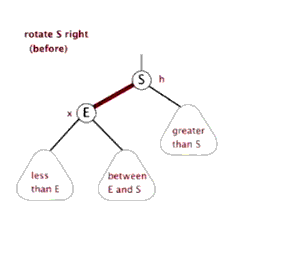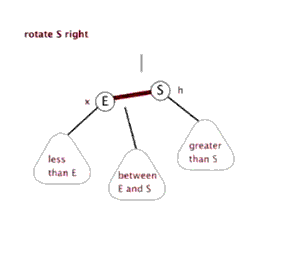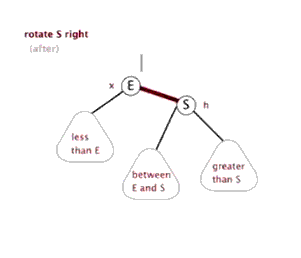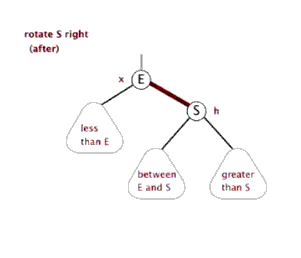
实现代码:
/**
* 排序树右旋转
*/
private void rightRotate() {
// 1.创建新节点,与根节点值相同
BinarySortTreeNode node = new BinarySortTreeNode(root.val);
//2.让新节点右子节点指向根节点右子节点
node.right = root.right;
//3.让新节点的左子节点指向根节点的左子节点的右子节点
node.left = root.left.right;
//4.让根节点的值变为其左子节点的值
root.val = root.left.val;
//5.把根节点的左子节点指向其左子节点的左子节点
root.left = root.left.left;
//6.让根节点的右子节点指向新节点
root.right = node;
}
/**
* 重写二叉排序树的节点添加方法,当添加完节点后左子树与右子树高度差大于1时,让树进行左旋转,若情况相反则进行右旋转
* @param node
*/
@Override
public void add(BinarySortTreeNode node) {
super.add(node);
//添加完节点后,判断左右树高度差是否大于1
int disparity = getRightHeight(root) - getLeftHeight(root);
if (disparity > 1) {
System.out.println("高度差:" + disparity + ",左旋转!");
//左子树与右子树高度差大于1就左旋
leftRotate();
}else if (- disparity > 1){
//右子树与左子树高度差小于1就左旋
rightRotate();
}
}
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 [email protected] 举报,一经查实,本站将立刻删除。



