天线阵列模型
0. 前言
阵列信号处理基础本质上属于参数估计问题,和信道估计知识基本上别无二致。末学在这里整理了阵列信号处理的基础知识。
3. 天线阵列模型1
天线阵元之间的摆放位置影响着阵列接收信号的数学模型,不同的天线阵列模型有着不一样的应用场景,并影响着阵列信号处理的方法。
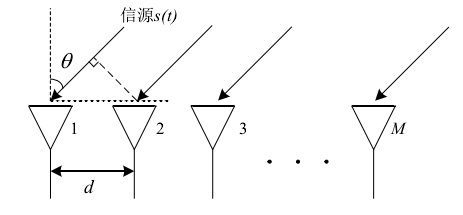
3.1 均匀线阵
假设
M
M
M 个阵元等距离排列成一条直线,阵元间距为
d
d
d。假设选取最左边的天线阵元作为参考点,则第
m
m
m 个天线阵元相对于参考点的时间延迟可以表示为
τ
m
(
θ
i
)
=
(
m
−
1
)
d
sin
θ
i
v
\tau_m(\theta_i) = \frac{(m-1)d \sin \theta_i}{v}
τm(θi)=v(m−1)dsinθi
-
各天线阵元之间的互耦效应忽略不计,且阵元间距为最高频率源信号的半波长,即 d = λ 2 d=\frac{\lambda}{2} d=2λ。
-
传播距离远大于阵列大小,即信号在介质中以平面波的形式到达阵列。
-
接收机各个通道拥有完全相同的特性。
根据以上假设,方向向量可以写为
a
(
θ
i
)
=
[
1
,
e
j
π
sin
θ
i
,
e
j
2
π
sin
θ
i
,
⋯
,
e
j
(
M
−
1
)
π
sin
θ
i
]
T
\mathbf{a}(\theta_i) = \left[1,e^{j\pi \sin \theta_i},e^{j2\pi \sin \theta_i},\cdots,e^{j(M-1)\pi \sin \theta_i} \right]^T
a(θi)=[1,ejπsinθi,ej2πsinθi,⋯,ej(M−1)πsinθi]T
在这里很尴尬地说,我用了好久的模型都是
e
−
j
(
k
−
1
)
π
β
i
e^{-j(k-1)\pi \beta_i}
e−j(k−1)πβi,今天才发现如果参考点为第一个阵元在最左边的话,指数应该是没有符号的,也就是上面的式子是正确的!
%%
当然,如果是如下图这种,参考阵元第一个在最右边,从右往左建模,则需要加符号!
%%
updated by 2019/7/19

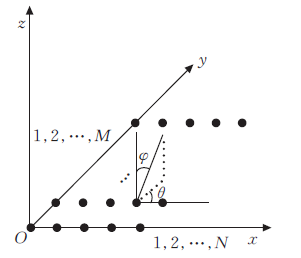
3.2 L 型阵
如图为 L 型阵列模型,在
x
x
x 轴和
y
y
y 轴均
M
M
M 个阵元,阵元间距为
d
d
d。
K
K
K 个信源,二维入射角为
(
θ
i
,
φ
i
)
(\theta_i,\varphi_i)
(θi,φi)。
x
x
x 轴上的接收信号模型可以视为线性阵列,
y
y
y 轴同理:
X
=
A
x
S
+
N
x
Y
=
A
y
S
+
N
y
\begin{aligned} X &= A_xS+N_x \\ Y &= A_yS+N_y \end{aligned}
XY=AxS+Nx=AyS+Ny
其中,方向矩阵为
A
x
=
[
a
x
(
θ
1
,
φ
1
)
,
⋯
,
a
x
(
θ
K
,
φ
K
)
]
A
y
=
[
a
y
(
θ
1
,
φ
1
)
,
⋯
,
a
y
(
θ
K
,
φ
K
)
]
a
x
(
θ
i
,
φ
i
)
=
[
1
,
e
−
j
2
π
λ
d
cos
θ
i
sin
φ
i
,
⋯
,
e
−
j
2
π
λ
(
M
−
1
)
d
cos
θ
i
sin
φ
i
]
T
a
y
(
θ
i
,
φ
i
)
=
[
1
,
e
−
j
2
π
λ
d
sin
θ
i
sin
φ
i
,
⋯
,
e
−
j
2
π
λ
(
M
−
1
)
d
sin
θ
i
sin
φ
i
]
T
\begin{aligned} A_x &= \left[a_x(\theta_1,\varphi_1),\cdots,a_x(\theta_K,\varphi_K)\right] \\ A_y &= \left[a_y(\theta_1,\varphi_1),\cdots,a_y(\theta_K,\varphi_K)\right] \\ a_x(\theta_i,\varphi_i) &= \left[1,e^{-j\frac{2\pi}{\lambda}d \cos\theta_i \sin\varphi_i},\cdots,e^{-j\frac{2\pi}{\lambda}(M-1)d \cos\theta_i \sin\varphi_i}\right]^T \\ a_y(\theta_i,\varphi_i) &= \left[1,e^{-j\frac{2\pi}{\lambda}d \sin\theta_i \sin\varphi_i},\cdots,e^{-j\frac{2\pi}{\lambda}(M-1)d \sin\theta_i \sin\varphi_i}\right]^T \end{aligned}
AxAyax(θi,φi)ay(θi,φi)=[ax(θ1,φ1),⋯,ax(θK,φK)]=[ay(θ1,φ1),⋯,ay(θK,φK)]=[1,e−jλ2πdcosθisinφi,⋯,e−jλ2π(M−1)dcosθisinφi]T=[1,e−jλ2πdsinθisinφi,⋯,e−jλ2π(M−1)dsinθisinφi]T
3.3 均匀平面阵
假设有 K K K 个信号源,均匀平面阵列指的是 M M M 个天线阵元等间距的排列成一个正方形或者矩形,如上图所示由 M × N M\times N M×N 个阵元组成。 x x x 轴方向有 N N N 个间距为 d d d 的均匀线阵, y y y 轴方向有 M M M 个间距为 d d d 的均匀线阵。如果选取原点为参考点,另外某个阵元的坐标可以写为 ( x n , y m ) (x_n,y_m) (xn,ym),于是时延差可以写为
τ
n
,
m
(
φ
k
,
θ
k
)
=
x
n
sin
φ
k
cos
θ
k
+
y
m
sin
φ
k
sin
θ
k
v
a
n
,
m
(
φ
k
,
θ
k
)
=
exp
(
−
j
w
0
τ
n
,
m
(
φ
k
,
θ
k
)
)
X
=
A
S
+
N
S
=
[
s
1
(
t
)
,
⋯
,
s
K
(
t
)
]
T
∈
C
K
×
1
A
=
[
a
(
θ
1
,
φ
1
)
,
⋯
,
a
(
θ
K
,
φ
K
)
]
∈
C
N
M
×
K
\begin{aligned} \tau_{n,m}(\varphi_k,\theta_k) &= \frac{x_n\sin\varphi_k\cos\theta_k + y_m\sin\varphi_k\sin\theta_k}{v}\\ a_{n,m}(\varphi_k,\theta_k) &= \exp\left(-jw_0\tau_{n,m}(\varphi_k,\theta_k)\right) \\ X &= AS+N \\ S &= \left[s_1(t),\cdots,s_K(t)\right]^T \in \mathbb{C}^{K \times 1}\\ A &= \left[a(\theta_1,\varphi_1),\cdots,a(\theta_K,\varphi_K)\right] \in \mathbb{C}^{NM \times K} \end{aligned}
τn,m(φk,θk)an,m(φk,θk)XSA=vxnsinφkcosθk+ymsinφksinθk=exp(−jw0τn,m(φk,θk))=AS+N=[s1(t),⋯,sK(t)]T∈CK×1=[a(θ1,φ1),⋯,a(θK,φK)]∈CNM×K
简单解释下这里的时延差公式怎么来的:
由之前的 ULA 基础可知,沿着入射波方向的长度差等于阵元
(
x
n
,
y
m
)
(x_n,y_m)
(xn,ym) 到原点直连距离
r
r
r 乘以入射波与平面阵法线的夹角角度的正弦
sin
φ
k
\sin \varphi_k
sinφk。
即这段沿着入射波方向的长度差为
r
⋅
sin
φ
k
r\cdot \sin \varphi_k
r⋅sinφk。而在
x
o
y
xoy
xoy 平面上,
x
n
2
+
y
m
2
=
r
2
x
n
=
r
cos
θ
k
y
m
=
r
sin
θ
k
\begin{aligned} x_n^2+y_m^2 &= r^2 \\ x_n &= r \cos \theta_k \\ y_m &= r \sin \theta_k \end{aligned}
xn2+ym2xnym=r2=rcosθk=rsinθk
于是就有
r
=
r
(
cos
2
θ
k
+
sin
2
θ
k
)
=
r
cos
θ
k
⋅
cos
θ
k
+
r
sin
θ
k
⋅
sin
θ
k
=
x
n
cos
θ
k
+
y
m
sin
θ
k
\begin{aligned} r&=r(\cos^2 \theta_k+\sin^2 \theta_k) \\ &=r \cos \theta_k \cdot \cos \theta_k + r \sin \theta_k \cdot \sin \theta_k \\ &=x_n \cos \theta_k+ y_m \sin \theta_k \end{aligned}
r=r(cos2θk+sin2θk)=rcosθk⋅cosθk+rsinθk⋅sinθk=xncosθk+ymsinθk
从
x
x
x 轴对应的
N
N
N 个阵元的方向矩阵和从
y
y
y 轴对应的
M
M
M 个阵元的方向矩阵为
A
x
=
[
a
x
(
θ
1
,
φ
1
)
,
⋯
,
a
x
(
θ
K
,
φ
K
)
]
A
y
=
[
a
y
(
θ
1
,
φ
1
)
,
⋯
,
a
y
(
θ
K
,
φ
K
)
]
a
x
(
θ
i
,
φ
i
)
=
[
1
,
e
−
j
2
π
λ
d
cos
θ
i
sin
φ
i
,
⋯
,
e
−
j
2
π
λ
(
N
−
1
)
d
cos
θ
i
sin
φ
i
]
T
a
y
(
θ
i
,
φ
i
)
=
[
1
,
e
−
j
2
π
λ
d
sin
θ
i
sin
φ
i
,
⋯
,
e
−
j
2
π
λ
(
M
−
1
)
d
sin
θ
i
sin
φ
i
]
T
\begin{aligned} A_x &= \left[a_x(\theta_1,\varphi_1),\cdots,a_x(\theta_K,\varphi_K)\right] \\ A_y &= \left[a_y(\theta_1,\varphi_1),\cdots,a_y(\theta_K,\varphi_K)\right] \\ a_x(\theta_i,\varphi_i) &= \left[1,e^{-j\frac{2\pi}{\lambda}d \cos\theta_i \sin\varphi_i},\cdots,e^{-j\frac{2\pi}{\lambda}(N-1)d \cos\theta_i \sin\varphi_i}\right]^T \\ a_y(\theta_i,\varphi_i) &= \left[1,e^{-j\frac{2\pi}{\lambda}d \sin\theta_i \sin\varphi_i},\cdots,e^{-j\frac{2\pi}{\lambda}(M-1)d \sin\theta_i \sin\varphi_i}\right]^T \end{aligned}
AxAyax(θi,φi)ay(θi,φi)=[ax(θ1,φ1),⋯,ax(θK,φK)]=[ay(θ1,φ1),⋯,ay(θK,φK)]=[1,e−jλ2πdcosθisinφi,⋯,e−jλ2π(N−1)dcosθisinφi]T=[1,e−jλ2πdsinθisinφi,⋯,e−jλ2π(M−1)dsinθisinφi]T
则可以得到方向矩阵
X
=
A
S
+
N
S
=
[
s
1
(
t
)
,
⋯
,
s
K
(
t
)
]
T
∈
C
K
×
1
A
=
[
a
(
θ
1
,
φ
1
)
,
⋯
,
a
(
θ
K
,
φ
K
)
]
=
[
A
x
D
1
(
A
y
)
A
x
D
2
(
A
y
)
⋮
A
x
D
M
(
A
y
)
]
∈
C
N
M
×
K
\begin{aligned} X &= AS+N \\ S &= \left[s_1(t),\cdots,s_K(t)\right]^T \in \mathbb{C}^{K \times 1}\\ A &= \left[a(\theta_1,\varphi_1),\cdots,a(\theta_K,\varphi_K)\right] \\ &= \begin{bmatrix} A_x D_1(A_y) \\ A_x D_2(A_y) \\ \vdots \\ A_x D_M(A_y) \end{bmatrix} \in \mathbb{C}^{NM \times K} \end{aligned}
XSA=AS+N=[s1(t),⋯,sK(t)]T∈CK×1=[a(θ1,φ1),⋯,a(θK,φK)]=⎣
⎡AxD1(Ay)AxD2(Ay)⋮AxDM(Ay)⎦
⎤∈CNM×K
其中
D
i
(
⋅
)
D_i(\cdot)
Di(⋅) 表示取矩阵的第
i
i
i 行作为构成对角矩阵的对角元素。
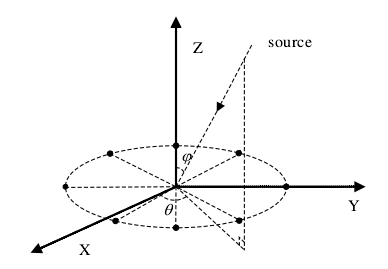
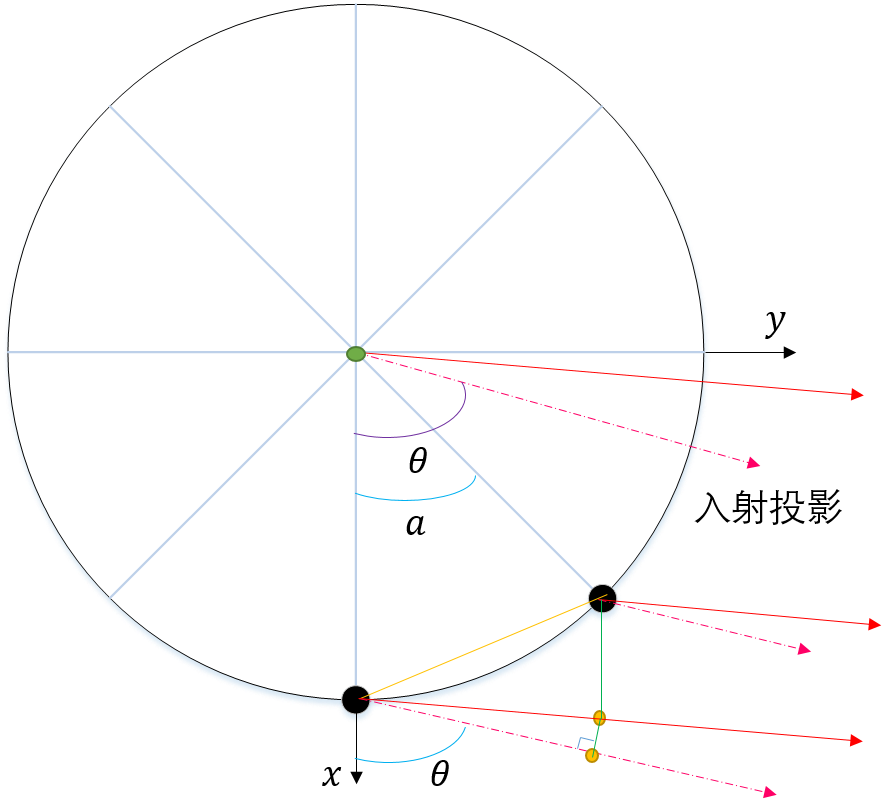
3.4 均匀圆阵
如图所示为均匀圆阵模型, M M M 个阵元均匀分布在圆周上,假设 K K K 个信源,二维入射角为 ( θ i , φ i ) (\theta_i,\varphi_i) (θi,φi),一般取圆周上两个阵元的间距为 λ / 2 \lambda/2 λ/2,对应的圆半径取为 R = λ 4 / sin ( π M ) R = \frac{\lambda}{4} / \sin(\frac{\pi}M) R=4λ/sin(Mπ),阵列的第 m m m 个阵元与 x x x 轴的角度用 2 π M ⋅ ( m − 1 ) \frac{2\pi}{M}\cdot (m-1) M2π⋅(m−1) 表示。
以原点为参考点,则位于
x
x
x 轴正方向的阵元视为沿着半径方向为轴的参考系。则有时延差:
τ
m
=
1
,
i
=
R
sin
φ
i
cos
θ
i
v
\tau_{m=1,i} = \frac{R \sin\varphi_i \cos\theta_i}{v}
τm=1,i=vRsinφicosθi
其中
θ
i
\theta_i
θi 是入射投影与半径方向的轴之间的夹角。同理第
m
m
m 个阵元即把阵元与原点之间的半径方向作为参考轴,此时入射投影与半径方向的轴之间的夹角为
θ
i
−
2
π
(
m
−
1
)
M
\theta_i-\frac{2\pi(m-1)}{M}
θi−M2π(m−1)。则有时延差:
τ
m
,
i
=
R
sin
φ
i
cos
(
θ
i
−
2
π
(
m
−
1
)
M
)
v
\tau_{m,i} = \frac{R \sin\varphi_i \cos\left(\theta_i-\frac{2\pi(m-1)}{M}\right)}{v}
τm,i=vRsinφicos(θi−M2π(m−1))
于是阵列方向向量为
A
=
[
a
(
θ
1
,
φ
1
)
,
⋯
,
a
(
θ
K
,
φ
K
)
]
a
(
θ
i
,
φ
i
)
=
[
exp
(
−
j
2
π
R
sin
φ
i
cos
(
θ
i
)
)
exp
(
−
j
2
π
R
sin
φ
i
cos
(
θ
i
−
2
π
M
)
)
⋮
exp
(
−
j
2
π
R
sin
φ
i
cos
(
θ
i
−
2
π
(
M
−
1
)
M
)
)
]
\begin{aligned} A &= \left[a(\theta_1,\varphi_1),\cdots,a(\theta_K,\varphi_K)\right] \\ a(\theta_i,\varphi_i) &= \begin{bmatrix} \exp\left(-j2\pi R\sin\varphi_i \cos\left(\theta_i\right)\right) \\ \exp\left(-j2\pi R\sin\varphi_i \cos\left(\theta_i-\frac{2\pi}{M}\right)\right) \\ \vdots \\ \exp\left(-j2\pi R\sin\varphi_i \cos\left(\theta_i-\frac{2\pi(M-1)}{M}\right)\right) \end{bmatrix} \end{aligned}
Aa(θi,φi)=[a(θ1,φ1),⋯,a(θK,φK)]=⎣
⎡exp(−j2πRsinφicos(θi))exp(−j2πRsinφicos(θi−M2π))⋮exp(−j2πRsinφicos(θi−M2π(M−1)))⎦
⎤
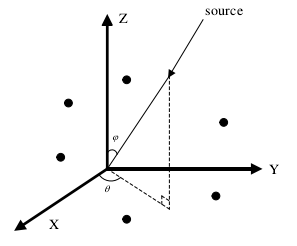
3.5 任意三维阵列天线模型
如图所示为任意阵列模型。假设
M
M
M 个阵元任意分布在空间中,二维入射角为
(
θ
i
,
φ
i
)
(\theta_i,\varphi_i)
(θi,φi),假设有
K
K
K 个信号源。则入射的方向矢量为:
V
=
[
sin
φ
i
cos
θ
i
sin
φ
i
sin
θ
i
cos
φ
i
]
T
\mathbf{V} = \begin{bmatrix} \sin\varphi_i\cos\theta_i & \sin\varphi_i\sin\theta_i & \cos\varphi_i \end{bmatrix}^T
V=[sinφicosθisinφisinθicosφi]T
如果第
m
m
m 个阵元的坐标位置为
r
m
=
(
x
m
,
y
m
,
z
m
)
\mathbf{r}_m = ( x_m, y_m, z_m)
rm=(xm,ym,zm) ,波速为
v
v
v。那么
τ m ( θ i , φ i ) = 1 v ( x m sin φ i cos θ i + y m sin φ i sin θ i + z m cos φ i ) \tau_{m}(\theta_i,\varphi_i) = \frac{1}{v} \left(x_m \sin\varphi_i\cos\theta_i + y_m \sin\varphi_i\sin\theta_i+ z_m \cos\varphi_i\right) τm(θi,φi)=v1(xmsinφicosθi+ymsinφisinθi+zmcosφi)
因此可得导向矢量:
a
(
θ
i
,
φ
i
)
=
[
p
1
(
θ
i
,
φ
i
)
exp
(
j
2
π
λ
r
1
⋅
V
)
p
2
(
θ
i
,
φ
i
)
exp
(
j
2
π
λ
r
2
⋅
V
)
⋮
p
M
(
θ
i
,
φ
i
)
exp
(
j
2
π
λ
r
M
⋅
V
)
]
\mathbf{a}(\theta_i,\varphi_i) = \begin{bmatrix} p_1(\theta_i,\varphi_i) \exp(j \frac{2\pi}{\lambda} \mathbf{r}_1 \cdot \mathbf{V}) \\ p_2(\theta_i,\varphi_i) \exp(j \frac{2\pi}{\lambda} \mathbf{r}_2 \cdot \mathbf{V}) \\ \vdots\\ p_M(\theta_i,\varphi_i) \exp(j \frac{2\pi}{\lambda} \mathbf{r}_M \cdot \mathbf{V}) \end{bmatrix}
a(θi,φi)=⎣
⎡p1(θi,φi)exp(jλ2πr1⋅V)p2(θi,φi)exp(jλ2πr2⋅V)⋮pM(θi,φi)exp(jλ2πrM⋅V)⎦
⎤
对于传统阵列,通常极化矢量
p
k
(
θ
,
φ
)
=
1
p_k(\theta,\varphi) =1
pk(θ,φ)=1 一般省略。但是对于极化敏感阵列,不同载体的影响产生屏蔽效应,所以
p
k
(
θ
,
φ
)
p_k(\theta,\varphi)
pk(θ,φ) 不能省略。
定义传统阵列方向矩阵为: A = [ a ( θ 1 , φ 1 ) , ⋯ , a ( θ K , φ K ) ] A = \left[a(\theta_1,\varphi_1),\cdots,a(\theta_K,\varphi_K)\right] A=[a(θ1,φ1),⋯,a(θK,φK)]。
参考文献
-
毫米波低复杂度 DOA 估计与波束成形技术的研究 ↩︎
版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 dio@foxmail.com 举报,一经查实,本站将立刻删除。