目录
LeNet
1998 年 11 月 8 日,杨立昆(Yann LeCun)为世界带来了第一个正式的卷积神经网络,他是一名知名计算机科学家,Facebook 首席人工智能科学家,2018 年图灵奖得主;他在机器学习、计算机视觉、移动机器人等领域都有贡献。
杨立昆创造的这个早期经典卷积神经网络叫什么名字?
| A | LeNet-3 |
| B | LeNet-2 |
| C | LeNet-5 |
| D | LeNet-4 |
答案:LeNet-5
编程牛人的盲点
Guy Steele 从 70 年代起就活跃于编程语言领域,他是 Scheme 的创始人、Sun Java 团队的成员、Emacs 部分命令的最初设计者;他也是《Common Lisp: the Language》的作者。 下面哪个计算机语言是他最不熟悉的:
| A | C |
| B | C++ |
| C | COBOL |
| D | C# |
答案:C#
你了解你身边的这个工具吗?
Ping 是一个常用的网络工具, 它Ping 是一个著名的命令行实用工具,用于测试 LAN 和 WAN 中设备之间的连接性和可达性,Ping 可以向指定的 URL 或 IP 地址发送一个 ICMP (Internet Control Message Protocol)回显请求包,并期望目标主机发送一个 ICMP 回显应答。如果收到目标主机的应答,则表明该主机仍在运行。 Ping 的全名是什么?
| A | Ping |
| B | Packet InterNet Groper |
| C | Ping Is Not Groper |
| D | Probe Internet NG |
答案:Packet InterNet Groper
好数对
已知一个集合A,对A中任意两个不同的元素求和,若求得的和仍在A内,则称其为好数对。例如,集合A={1 2 3 4},1+2=3,1+3=4,则1,2和1,3 是两个好数对。编写程序求给定集合中好数对的个数。 注:集合中最多有1000个元素,元素最大不超过10000 程序运行示例1:
4↙
1 2 3 4↙
2
```
程序运行示例2:
```json
7↙
2456 3251 654 890 100 754 1234↙
1
```
其中,“↙”表示输入
以下程序实现了这一功能,请你填补空白处内容:
```cpp
#include <stdio.h>
#include <stdlib.h>
int main()
{
int n, i, j, t;
scanf("%d", &n);
int *a = (int *)malloc(n * sizeof(int));
for (i = 0; i < n; i++)
{
scanf("%d", &a[i]);
}
int cout = 0;
for (i = 0; i < n; i++)
{
for (j = i + 1; j < n; j++)
{
for (t = 0; t < n; t++)
____________;
}
}
printf("%d", cout);
free(a);
return 0;
}| A | if (a[i] + a[j] <= a[t]) cout++; |
| B | if (a[i] + a[j] < a[t]) cout++; |
| C | if (a[i] + a[j] >= a[t]) cout++; |
| D | if (a[i] + a[j] == a[t]) cout++; |
答案:
if (a[i] + a[j] == a[t])
cout++;不同路径
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
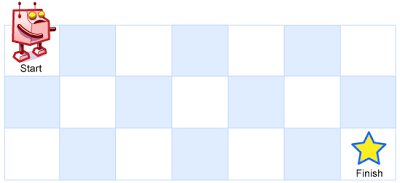
输入:m = 3, n = 7 输出:28
示例 2:
输入:m = 3, n = 2 输出:3 解释:从左上角开始,总共有 3 条路径可以到达右下角。 1. 向右 -> 向下 -> 向下 2. 向下 -> 向下 -> 向右 3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3 输出:28
示例 4:
输入:m = 3, n = 3 输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
#include <stdio.h>
#include <stdlib.h>
static int uniquePaths(int m, int n)
{
int row, col;
int *grids = malloc(m * n * sizeof(int));
for (col = 0; col < m; coL++)
{
grids[col] = 1;
}
for (row = 0; row < n; row++)
{
grids[row * m] = 1;
}
for (row = 1; row < n; row++)
{
for (col = 1; col < m; coL++)
{
______________________________;
}
}
return grids[m * n - 1];
}
int main(int argc, char **argv)
{
if (argc != 3)
{
fprintf(stderr, "Usage: ./test m n\n");
exit(-1);
}
printf("%d\n", uniquePaths(atoi(argv[1]), atoi(argv[2])));
return 0;
}| A | grids[row * m + col] = grids[row * m + col] + grids[row * m + col]; |
| B | grids[row * m + col] = grids[row * m + col - 1] + grids[(row - 1) * m + col]; |
| C | grids[row * m + col] = grids[row * m + col - 1] + grids[row * m + col + 1]; |
| D | grids[row * m + col] = grids[row * m + col + 1] + grids[row * m + col]; |
答案:
grids[row * m + col] = grids[row * m + col - 1] + grids[(row - 1) * m + col];N皇后 II
n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
给你一个整数 n ,返回 n 皇后问题 不同的解决方案的数量。
示例 1:
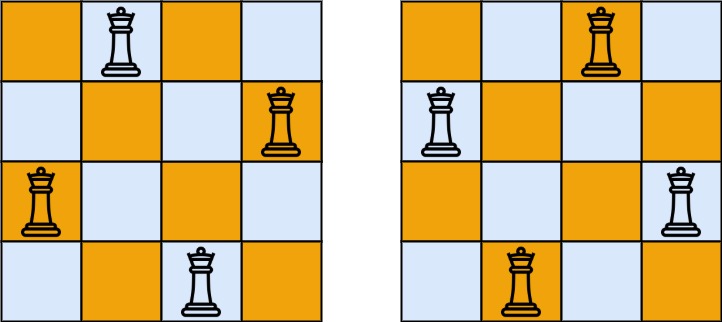
输入:n = 4 输出:2 解释:如上图所示,4 皇后问题存在两个不同的解法。
示例 2:
输入:n = 1 输出:1
提示:
1 <= n <= 9- 皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
#include <bits/stdc++.h>
using namespace std;
class Solution
{
public:
int totalNQueens(int n)
{
vector<int> stack(n);
return dfs(n, 0, stack);
}
private:
int dfs(int n, int row, vector<int> &stack)
{
int count = 0;
if (row == n)
{
return count + 1;
}
else
{
for (int i = 0; i < n; i++)
{
if (row == 0 || !conflict(stack, row, i))
{
stack[row] = i;
_______________________;
}
}
return count;
}
}
bool conflict(vector<int> &stack, int row, int col)
{
for (int i = 0; i < row; i++)
{
if (col == stack[i] || abs(row - i) == abs(col - stack[i]))
{
return true;
}
}
return false;
}
}
| A | count += dfs(n, row - 1, stack); |
| B | count += dfs(n, row + 1, stack); |
| C | count += dfs(n, row, stack); |
| D | count += dfs(n + 1, row, stack); |
答案:
count += dfs(n, row + 1, stack);版权声明:本文内容由互联网用户自发贡献,该文观点与技术仅代表作者本人。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如发现本站有涉嫌侵权/违法违规的内容, 请发送邮件至 dio@foxmail.com 举报,一经查实,本站将立刻删除。




